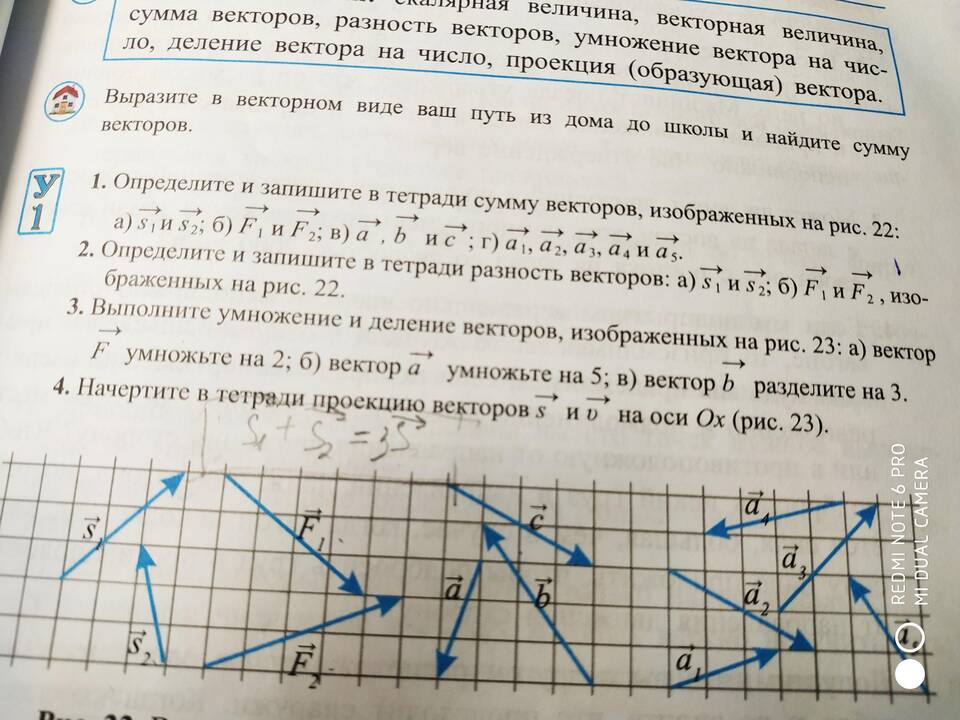
Для определения суммы векторов, представленных графически, необходимо использовать правила векторного сложения. Рассмотрим основные методы решения этой задачи.
Содержание
Основные правила сложения векторов
| Метод | Описание |
| Правило треугольника | Конец первого вектора соединяется с началом второго |
| Правило параллелограмма | Векторы откладываются от общей точки |
| Многоугольника | Последовательное соединение нескольких векторов |
Пошаговая инструкция для определения суммы
- Определите координаты начала и конца каждого вектора на рисунке
- Вычислите проекции каждого вектора на оси координат
- Сложите соответствующие проекции всех векторов
- По полученным суммам проекций постройте результирующий вектор
Аналитический метод расчета
Если известны координаты векторов:
| Вектор | Проекция на OX | Проекция на OY |
| a | ax | ay |
| b | bx | by |
| Сумма a + b | ax + bx | ay + by |
Графическое представление сложения
Для двух векторов:
- Отложите первый вектор от произвольной точки
- К его концу приложите начало второго вектора
- Суммой будет вектор от начала первого к концу второго
Для нескольких векторов:
- Последовательно соединяйте векторы "конец к началу"
- Замыкающий вектор от начала первого к концу последнего даст сумму
Пример вычисления суммы
Даны три вектора с координатами:
- a = (2, 3)
- b = (-1, 2)
- c = (4, -1)
Их сумма:
| Ось | Расчет | Результат |
| OX | 2 + (-1) + 4 | 5 |
| OY | 3 + 2 + (-1) | 4 |
Результирующий вектор: (5, 4)
Особые случаи
| Ситуация | Результат |
| Сумма противоположных векторов | Нулевой вектор |
| Сложение коллинеарных векторов | Вектор той же направленности |
| Сложение перпендикулярных векторов | Диагональ прямоугольника |
Практическое применение
- Физика (сложение сил, скоростей)
- Компьютерная графика
- Навигация и картография
- Инженерные расчеты